Looking at my posts so far, I haven’t been talking about math yet. So today I’m starting a new series on my favorite part of math: Fourier analysis.
Now please my dear readers (both of you), don’t run away! This isn’t about the formal parts. What I actually want to talk about is how intuitions transfer to abstract calculations we wouldn’t expect them to transfer to. Specifically, the Fourier transform is like a base change and base changes work by projection. If you understood that sentence you’ll probably find the series boring, because it’s all about explaining it.
For those still reading, first I’ll give a big picture explanation of what Fourier analysis is.
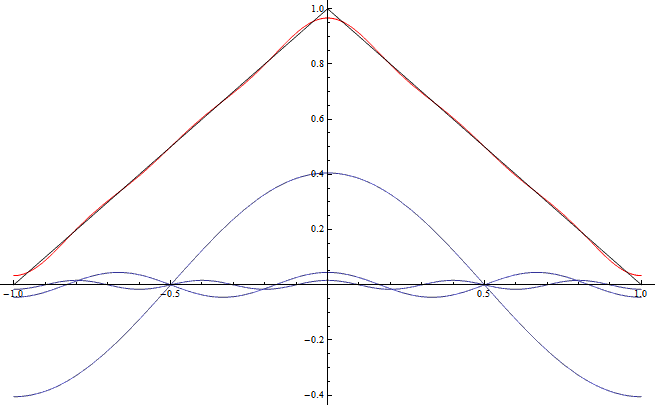
The black triangular graph in this picture is mostly covered by the red graph approximating it. The function plotted in red is the sum of the three functions plotted in blue, all of which are cosines. With more cosines I would get an even better approximation of the triangle.
It gets interesting because I actually started with the triangular graph and calculated which cosines I had to use to make this picture. Such a calculation can be made for many more functions. Basically if you can plot a function without lifting your pen and it either repeats infinitely or goes to a constant at both sides of your plot, then if you give me enough cosines and sines I can make them add up to a good approximation of that function. In the limit of infinitely many cosines and sines they add up to the function itself.
One application of this is in string instruments: you probably remember waves can spread on the strings and from them through the air as sounds. But when you pluck a string you actually bring it in a triangular form that doesn’t look wavey at all. You can see the solution in my plot above: The triangle is a sum of lots of cosines that actually do look wavey. And if you look at the plot again, there is one cosine much bigger than the others. (Of much larger amplitude if you want to get pedantic.) That one corresponds to the string’s tone. The smaller ones correspond to what musicians call overtones.
If that isn’t cool enough, I’ll say with only slight overstatement that quantum mechanics is all made up of applications of Fourier analysis.
Fine, so lots of functions are sums of sines and cosines. But how do we get at the sines and cosines? You can easily find the formulas on the Internet (and maybe I’ll quote them later in the series) but actually I don’t want to talk about the formulas per se; I want to talk about intuitive analogies they can be understood by.
It will turn out that Fourier analysis is a lot like the geometry of shadows. To explain that I’ll first have to talk about geometry and shadows.
Yep, it’s a cliffhanger.
Index to the series:
1. This post.
2. Vectors.
3. …